Edit Distance Calculation - Recursive Edit Distance of Prefixes

Say we want to calculate the edit distance between two strings X and Y.

Recall that the edit distance is “the least number of operations (substitution, insertion or deletion) needed to turn X into Y”.

It might not be that straightforward to come up with a solution to that. The key is to break the problem down to smaller subproblem, solve for the slightly smaller problem, and build upon that solution.

Here we reduce the problem to a slightly smaller scale by looking at the prefix of X and Y.

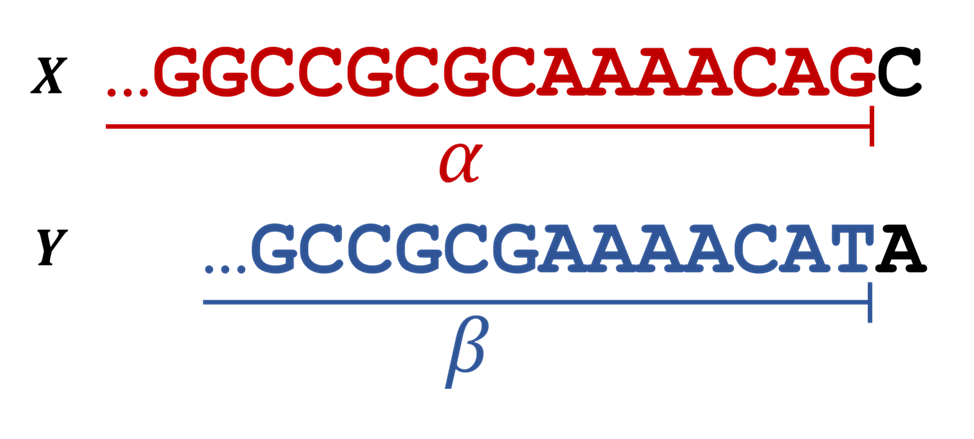
α and β are prefixes of X and Y, with only 1 character short, meaning X[:-1] andY[-1], respectively.

There are 3 ways turn X to Y

The edit distance between X and Y would be the minimum value of the 3 cases.

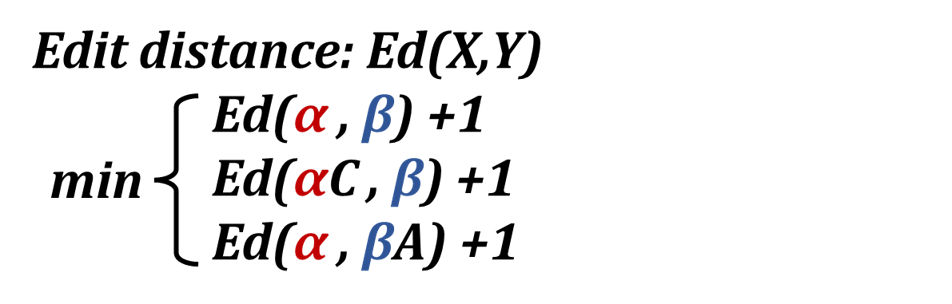
Note that in all 3 cases the edit distance problem becomes smaller, in case 1, we are solving the edit distance of strings that are one character shorter than X and Y, and in case 2 & 3 either X or Y gets trimmed down by one character.

In the general case, instead of the last character in X and Y being C and A, they could be any letter x and y, in which case we need to change the first equation from “+1” to “+δ(x,y)”, meaning that a substitution is needed when x != y (δ function equals to 1), and no operation is needed when x == y (δ function equals to 0).

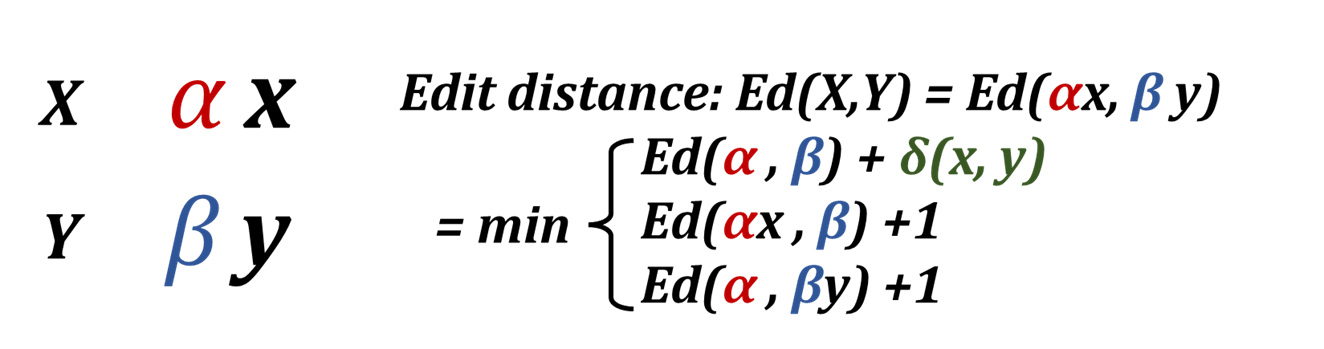
If we keep shortening the string(s) that we feed into the edit distance problem, even just by one character at each iteration, eventually either X or Y will be shortened all the way down to an empty string, which is the smallest/simplest problem we can reduce our system to.

And the answer to the simplest case is obvious: the edit distance of any string s with an empty string is the length of s.

To recap

• The problem of calculating the edit distance between X and Y can be solved by looking at smaller subproblems - the edit distance of prefixes of X and Y.
• In each subproblem, the length(s) of either X, Y or both XY are shortened by one.
• By recursively looking at the subproblem of the subproblem, eventually either X and Y becomes an empty string, the solution of that can be easily calculated.
• Then we can trace back each recursion to get the answer of the original problem.

Edit distance calculation in Python code

def edDistRecursive(a, b): 
	if len(a) == 0: return len(b) 
	if len(b) == 0: return len(a) 
	
	delt = 1 if a[-1] != b[-1] else 0 
	
	return min(edDistRecursive(a[:-1], b[:-1]) + delt, edDistRecursive(a[:-1], b) + 1, edDistRecursive(a, b[:-1]) + 1)